Açı, iki ışının (doğru parçası) başlangıç noktalarının kesişmesiyle oluşan geometrik şekildir. Bu iki ışının kesiştiği noktaya köşe, ışınların her birine ise kenar denir.
Açı Türleri
Dar Açı: Ölçüsü 0 ile 90 derece arasında olan açıdır. Örneğin, 30° veya 45°.
Dik Açı: Ölçüsü tam olarak 90 derece olan açıdır. İki kenarın birbirine dik olduğu açıdır.
Geniş Açı: Ölçüsü 90 ile 180 derece arasında olan açıdır. Örneğin, 120° veya 150°.
Doğru Açı: Ölçüsü tam olarak 180 derece olan açıdır. Düz bir çizgi üzerinde yer alan açı.
Tam Açı: Ölçüsü 360 derece olan açıdır. Tam bir daireyi kapsar.
Açıların Gösterimi
Açılar genellikle bir harf ile gösterilir, örneğin ∠ABC ifadesinde, B açının köşesidir.
Açının ölçüsü derece (°) cinsinden ifade edilir.
Yorum yapabilmek için giriş yapmalısınız.
Açı ölçüleri, bir açının büyüklüğünü ifade etmek için kullanılan
derecelerle (°) belirlenir. Açı ölçüleri, açıların türlerine göre değişiklik
gösterir. İşte başlıca açı ölçüleri ve türleri:
Sıfır
Açı (0°):
Açı ölçüsü 0° olan açıdır. İki ışın
veya doğru parçası aynı doğrultuda, üst üste çakışmış durumdadır. Geometrik
olarak iki ışın birbirine tam paraleldir.
Dar Açı (0° < A < 90°):
Açı ölçüsü 0° ile 90° arasında olan
açılardır. Dar açılar, dik açılardan küçük fakat sıfır açıdan büyüktür.
Örneğin, 30°, 45° gibi açılar dar açılara örnektir.
Dik Açı (90°):
Açı ölçüsü tam olarak 90° olan açıdır.
İki doğru parçası veya ışın birbirine dik bir şekilde kesiştiğinde dik açı
oluşur. Dik açı, genellikle kare ve dikdörtgen gibi şekillerde görülür.
Geniş Açı (90° < A < 180°):
Açı ölçüsü 90° ile 180° arasında olan
açılardır. Geniş açılar, dik açılardan büyük, doğru açılardan küçüktür.
Örneğin, 120°, 150° gibi açılar geniş açılara örnektir.
Doğru Açı (180°):
Açı ölçüsü tam olarak 180° olan açıdır.
İki ışın veya doğru parçası, düz bir doğru üzerinde uzanıyorsa, doğru açı
oluşur. Bu durumda, açı, bir doğru boyunca uzanır ve düz bir hat oluşturur.
Tam Açı (360°):
Açı ölçüsü tam olarak 360° olan açıdır.
Bir ışın başlangıç noktasından başlayarak tam bir daireyi tamamladığında
oluşur. Tam açı, bir tam dönüş veya daireyi ifade eder.
Refleks Açı (180° < A < 360°):
Açı ölçüsü 180° ile 360° arasında olan
açılardır. Refleks açılar, doğru açıdan büyük fakat tam açıdan küçüktür. Örneğin,
210°, 270° gibi açılar refleks açılara örnektir.
Bu açı ölçüleri, geometri ve trigonometri gibi matematiksel disiplinlerde sıkça kullanılır. Açıların büyüklüğü, şekillerin özelliklerini anlamada ve çeşitli mühendislik, mimarlık, fizik gibi alanlarda hesaplamalar yapmada önemli bir rol oynar.
Yorum yapabilmek için giriş yapmalısınız.
Üçgenin iç açıları ile ilgili bir paylaşım...
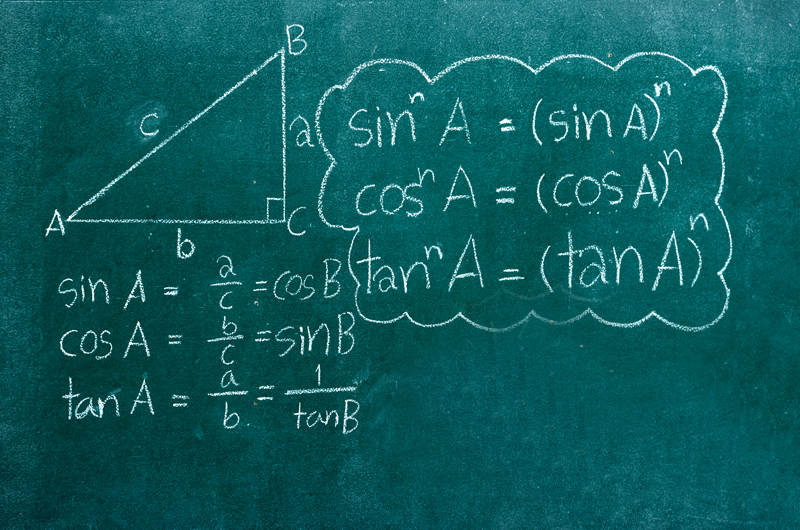
Yorum yapabilmek için giriş yapmalısınız.
Açı Denilince İlk Akla Gelenler
- Geometri ve Matematik:
- Temel Geometrik Kavram: Açı, geometri derslerinde ilk öğretilen temel kavramlardan biridir. İki doğru parçasının (veya ışının) kesiştiği noktada oluşan geometrik şekildir. Açı, iki ışının veya doğru parçasının arasındaki açılma miktarını ifade eder.
- Derece Ölçümü: Açıların ölçülmesi genellikle derece cinsindendir (°). Örneğin, dik açı 90°, tam açı 180°, ve doğru açı 360° olarak ölçülür.
- Açı Türleri: Dar açılar (0° ile 90° arasında), dik açılar (90°), geniş açılar (90° ile 180° arasında) ve tam açılar (180°) gibi farklı açı türleri vardır. Bu türler, geometri problemlerinde sıkça karşımıza çıkar.
- Açı Ölçme Araçları:
- İletki: Açı ölçme ve çiziminde kullanılan bir araçtır. İletki, genellikle yarım daire şeklinde olup 0° ile 180° arasında derece işaretleri bulunur.
- Gönye: Gönye, dik açılar oluşturmak ve ölçmek için kullanılan bir başka önemli geometri aracıdır.
- Trigonometri:
- Sinüs, Kosinüs, Tanjant: Trigonometri, açıların ölçülmesi ve hesaplanması üzerine kuruludur. Sinüs, kosinüs ve tanjant gibi trigonometri fonksiyonları, bir açının karşı ve komşu kenarlarına göre hesaplamalar yapar.
- Üçgenler ve Açı Hesapları: Trigonometri, özellikle üçgenlerin iç açıları ve kenar uzunlukları arasındaki ilişkileri anlamada kullanılır. Herhangi bir üçgende iç açılarının toplamı 180°dir.
- Uygulamalı Bilimler:
- Mühendislik ve Mimarlık: Açı kavramı, mühendislik ve mimarlıkta çok önemli bir rol oynar. Bina tasarımlarından köprü yapımına kadar birçok yapısal hesaplamada açılar kullanılır.
- Fizik: Fizikte açılar, kuvvetlerin yönlerini ve moment hesaplamalarını belirlemek için kullanılır. Vektör analizlerinde açılar kritik öneme sahiptir.
- Sanat ve Tasarım:
- Perspektif: Sanat ve tasarımda, perspektif çizimleri açılar kullanılarak yapılır. Nesnelerin doğru perspektifte çizilmesi için açılar önemlidir.
- Optik ve Işık: Işık ve gölge oyunlarında, ışığın geliş açısı, bir nesnenin nasıl görüneceğini belirler. Bu durum, hem sanat hem de optik bilimi açısından önemlidir.
- Günlük Hayat:
- Görüş Açısı: Günlük hayatta da açı kavramı sıkça kullanılır. Örneğin, bir kişinin görüş açısı, bir nesneyi hangi açılardan görebileceğini belirler.
- Fotoğrafçılık: Fotoğrafçılıkta, çekim açısı bir fotoğrafın kompozisyonunu ve estetiğini etkiler. Farklı açılardan çekilen fotoğraflar, farklı duygular ve anlamlar yaratır.
- İçsel ve Felsefi Anlam:
- Bakış Açısı: Açı kavramı, metaforik olarak da kullanılır. Bir konuya veya duruma nasıl yaklaştığınızı ifade eder. "Farklı açılardan bakmak" ifadesi, bir sorunu veya olayı farklı perspektiflerden değerlendirmeyi anlatır.
- Kişisel Açı: Kişisel açı, bireyin olaylara, insanlara veya yaşantılara karşı olan tutumunu ifade eder. Farklı insanlar aynı olaya farklı açılardan bakabilir ve farklı sonuçlara varabilir.



